2022年單招考試數學複習題
一、選擇題:(每題5分🥋,共28道🈂️🦠,共計140分)
1.方程 的解為( )
的解為( )
A. B.
B.  C.
C.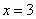 D.
D.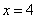

2.若 ,則
,則 的值為( )
的值為( )
A.0 B.1 C.-2 D.-3
3.用列舉法表示集合👰🏿♂️: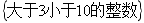 👳♂️,正確的是( )
👳♂️,正確的是( )
A.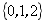 B.
B. C.
C. D.
D.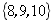
4. 的解集為( )
的解集為( )
A. B.
B.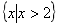 C.
C. D.
D.
5.函數 的定義域為( )
的定義域為( )
A.  B.
B.  C.
C.  D.
D.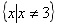
6.函數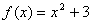 的值域是( )
的值域是( )
A. B.
B.  C.
C.  D.
D. 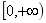
7.已知函數 在R上為偶函數,則
在R上為偶函數,則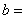 ( )
( )
A.0 B.1 C.2 D.-1
8.在指數函數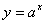 中,
中,  的取值範圍是( )
的取值範圍是( )
A.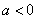 B.
B. C.
C. D.
D.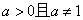
9.偶函數 在
在 上為減函數,最小值為7🦙,則
上為減函數,最小值為7🦙,則 在
在 上是( )
上是( )
A.增函數且最小值為7 B. 增函數且最大值為7
B. 減函數且最小值為7 D. 減函數且最大值為7
10.若 的大小關系是( )
的大小關系是( )
A.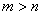 B.
B.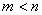 C.
C. D.無法確定
D.無法確定
11.已知 🧛🏼,則
🧛🏼,則 是
是 的( )
的( )
A.充分不必要條件 B.必要不充分條件
C.充要條件 D.既不充分也不必要條件
12.命題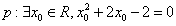 ,則命題
,則命題 的否定是( )
的否定是( )
A. 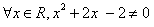 B.
B. 
C.  D.
D. 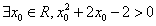
13.若方程x2-2mx+4=0的兩根滿足一根大于1,一根小于1,則m的取值範圍是( )
A.(-∞🐭🐩,-2) B.(-∞,-2)∪(2👰🏽♂️,+∞) C.(2🔎,+∞) D.(-2,+∞)
14.下列函數中,在區間(1,2)內有零點的函數是( )
A. B.
B. C.
C. D.
D.
15.sin14ºcos16º+cos14ºsin16º的值是( )
A.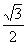 B.
B. C.
C. D.
D.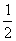
16.已知 🔸,且角的終邊在第二象限🧢,則
🔸,且角的終邊在第二象限🧢,則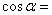 ( )
( )
A. B.
B.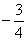 C.
C. 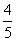 D.
D. 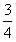
17.在 上滿足
上滿足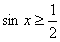 的
的 的取值範圍是( )
的取值範圍是( )
A.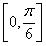 B.
B. C.
C.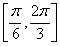 D.
D.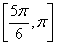
18.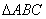 中,若
中,若 🦠,則
🦠,則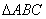 的面積為( )
的面積為( )
A. B.1 C.
B.1 C.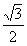 D.
D.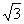
19.若→·→+→2=0🫄🏻,則△ABC必定是( )
A.銳角三角形 B.直角三角形 C.鈍角三角形 D.等腰直角三角形
20.已知向量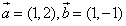 ,則
,則 ( )
( )
A.-1 B.3 C.(2🍪,1) D.(3🦏,0)
21.已知平面向量 ,則
,則 與
與 的夾角是( )
的夾角是( )
A. B.
B.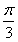 C.
C.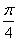 D.
D.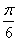
22.在等差數列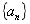 中🔼,
中🔼, 🧑🏼🍳,則
🧑🏼🍳,則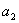 的值為( )
的值為( )
A.5 B.6 C.8 D.10
23.已知複數z滿足(1-i)z=2+i🧑🏻🍳,則z的共軛複數在複平面內對應的點在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
24.已知直線 及平面
及平面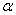 🤟🏽,下列命題中的假命題是( )
🤟🏽,下列命題中的假命題是( )
A.若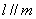 ,
, ,則
,則 .
.
B.若 ,
, ,則
,則 .
.
C.若 ,
, 🕞,則
🕞,則 .
.
D.若 💇♀️,
💇♀️, 🙋🏻♂️,則
🙋🏻♂️,則 .
.
25.直線x+y-2=0與圓x2+y2=4相交于A,B兩點,則弦AB的長度等于( )
A.2 B.2 C. D.1
26.已知圓柱的底面直徑與高 都等于球的直徑🍧,則圓柱的
都等于球的直徑🍧,則圓柱的 體積與球體積之比為( )
體積與球體積之比為( )
A.1∶2 B.2∶1 C.2∶3 D.3∶2
27.同時擲兩個骰子,其中向上的點數之和是5的概率( )
A.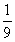 B.
B. C.
C. D.
D.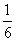
28.容量為20的樣本數據♦️👩🏼💼,分組後的頻數如下表🧑🏽🔬:則樣本數據落在區間[10,40)的頻率為( )
分組 |
[10,20) |
[20,30) |
[30,40) |
[40,50) |
[50,60) |
[60,70) |
頻數 |
2 |
3 |
4 |
5 |
4 |
2 |
A.0.35 B.0.45 C.0.55 D.0.65
二💹、填空題(每題5分🍰,共20道,共計100分)
1. _______
_______
2.若 互為相反數👨👦👦,則
互為相反數👨👦👦,則 ________
________
3. 已知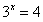 ,則
,則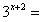 ______
______
4.設 ,則
,則
5.已知函數 ,若
,若 ,則
,則 =
=
6.若直角坐標內的點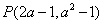 在第四象限,則
在第四象限,則 的取值範圍為____________
的取值範圍為____________
7.如果函數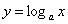 的圖象過點(9🦹🏽♂️,2),則
的圖象過點(9🦹🏽♂️,2),則 = ________
= ________
8.計算 =
=
9.已知 ,則角
,則角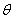 一定在第______象限
一定在第______象限
10.
11.已知函數 的最小正周期為
的最小正周期為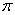 ,則
,則 .
.
12.若直線 ,則k=______
,則k=______
13. 在 軸上的截距為2且傾斜角為45°的直線方程為
軸上的截距為2且傾斜角為45°的直線方程為
14.已知x,y為正實數,且滿足4x+3y=12🧑🏼🎤,則xy的最大值為________.
15.若直線l1:ax+2y=0和直線l2🦍:2x+(a+1)y+1=0垂直,則實數a的值為________.
16. 等比數列
17.正方體 中💊,異面直線
中💊,異面直線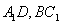 所成的角大小為
所成的角大小為
18.橢圓9+2=1的焦點為F1🧎♀️➡️💩,F2,點P在橢圓上.若|PF1|=4,則|PF2|=________
19. 8名世界網球頂級選手在上海大師賽上分成兩組,每組各4人,分別進行單循環賽,每組決出前兩名👨🦯➡️,再由每組的第一名與另一組的第二名進行淘汰賽,獲勝者角逐冠👮🏻♀️、亞軍👷🏻🧑🏻🦲,敗者角逐第3🍎、4名,大師賽共有________場比賽.
20.某田徑隊有男運動員30人,女運動員10人.用分層抽樣的方法從中抽出一個容量為20的樣本👩🏽🍼,則抽出的男運動員有 人.
三、解答題🤹🏻♀️:(每題10分,共6題😄,共計60分)
1.若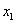 和
和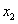 分別是一元二次方程
分別是一元二次方程 的兩根,求
的兩根,求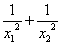 的值?
的值?
2.化簡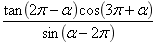
3.已知不等式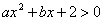 的解集為
的解集為 🧑🍼,求
🧑🍼,求 的解集👉🏽?
的解集👉🏽?
4.已知兩條平行直線 與
與 之間的距離是
之間的距離是 🤞🏽,求m+n的值?
🤞🏽,求m+n的值?
5.已知二次函數f(x)的圖像過點A(-1,0)、B(3,0)、C(1♗👩🏼🚒,-8).
(1)求f(x)的解析式⛵️;
(2)求f(x)在x∈[0,3]上的最值🤷♂️;
6.已知函數f(x)=2cos2x-sin xcos x-2sin2x.
(1)求f(x)的最小正周期🤸🏿;
(2)求f(x)的單調區間.
